Fast uncertainty estimation for mobilenet.

While writing my bachelor thesis, I often ended up using Detexify to look up latex symbols I forgot. Unfortunately, mobile data doesnt work very well in germany, so when I was traveling a lot of times I could'nt access this page. For this reason, I build Detext, a progressive web app (PWA), that classifies latex symbols without needing a internet connection. It uses MobileNet (Howard et al., 2017), which is run directly on the client side using onnx.js.

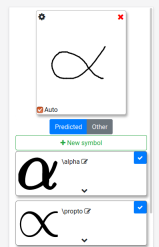
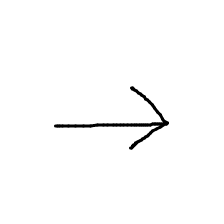
This works pretty well for most symbols. The only pet peeve I had with it until recently was, that it wont tell you when its not certain about the predicted symbol or simply predicts the wrong symbol. In the following example, the app predicts the \(\rightarrow\) (\rightarrow) symbol, since it does'nt know \(\rightharpoonup\) (\rightharpoonup).

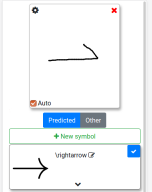
Ideally of course, the prediction would include some uncertainty of the network. This is known as uncertainty estimation and a variety of approaches exist to solve it, for example using model ensembles (Lakshminarayanan et al., 2017), predicting a uncertainty (Segu et al., 2019) or using test time dropout (Gal and Ghahramani, 2016).

In this article I will focus on test time dropout. Normally, dropout is only enabled during training and is used to prevent overfitting. To enable the model uncertainty, instead of disabling the dropout layers(s) during testing, one can instead keep it enabled. Feeding in the same input to a network with test time dropout will then give different outputs, depending on which neurons stay enabled.

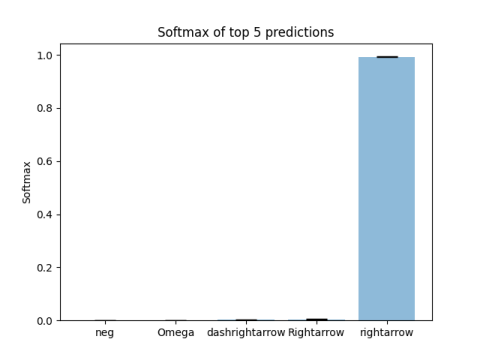
Lets look at an example. The top-5 softmax values that mobilenet predicts for the following picture

are shown in the plot below:

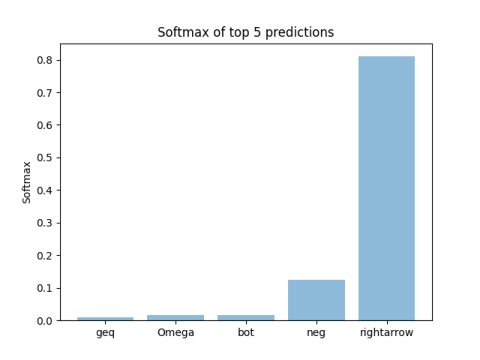
Since the \(\rightharpoonup\) symbol is not in the training dataset, these are all wrong of course. Unfortunately, the softmax score for the top class is pretty high, so it can not be used as an uncertainty estimate.

To estimate the model uncertainty, we turn on dropout at test time and look at the model predictions. For this we pass the same image through the network 100 times and visualize the predictions together with their variance:

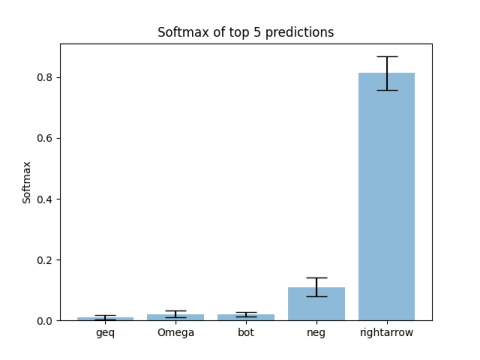
Here the black bars indicate the standard deviation of the predicted softmax values. We can see that using test time dropout induces some variance.

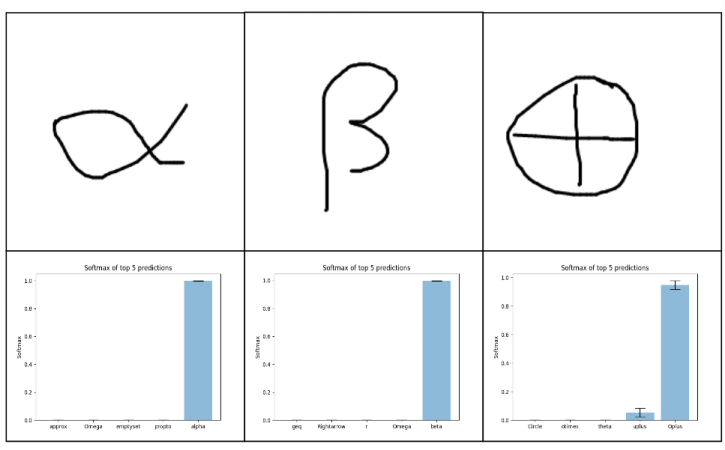
If we compare this to the prediction of a symbol that is included in the dataset, like the following

we can see that this has a lower variance:

.

Lets look at a few more examples. Here are the variances of symbols that are close to the training set:

.

And here those of pictures that are not found in the training set:

.

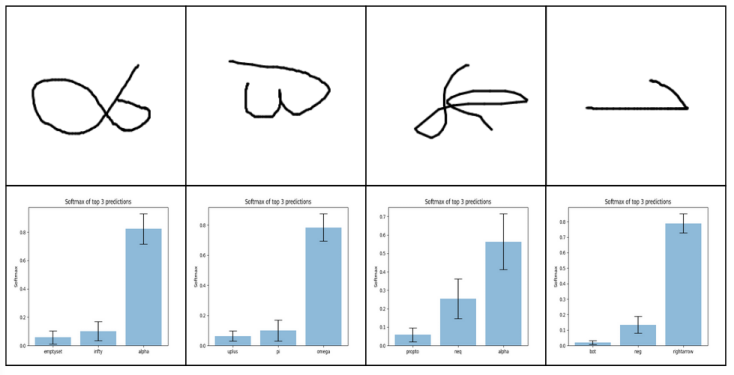This is nice, since it allows us to detect when the model is uncertain about its predictions. Unfortunately, this approach requires us to make multiple forward passes through the model. In the case of the Detext app this is not acceptable. The app should run on mobile devices too, and there a forward pass might already take ~1 second. Doing 10 forward passes just to estimate the uncertainty would take too long. Fortunately the architecture of mobilenet allows us to estimate the variance with only one forward pass.

The standard implementation of MobileNet only includes a single dropout layer. It computes a image feature with the feature network \(f: \mathbb{R}^{W \times H} \rightarrow \mathbb{R}^D\), then applies dropout and then used a single fully connected layer and a softmax, so in full the prediction of an image is

The feature of an image will thus always be the same, even with test time dropout enabled. We can use a few simple tricks to estimate the variance.

The covariance matrix \(\Sigma^F\) of \(F = dropout(f(image))\) is simply a diagonal matrix with \(\Sigma^F_{ii} = p/(1-p)*f(image)_i^2\) (its just a bernoully random vector multiplied by \(f(image)/(1-p)\) ).

We get the covariance after the linear layer by using the fact that \(X = W F\) has covariance \(W \Sigma^F W^T\). Now we only have to find out how to compute the variance of \(softmax(X)\) given the covariance and mean of \(X\).

We can do this using the taylor expansion for the moments of random variables. For the covariance this reads:

where \(J_f\) is the jacobian of \(f\) evaluated at \(E[X]\). We only need to find the jacobian of the softmax which is given by:

In total the evaluation of the variance is done by

Lets compare the variance we get with this estimate to the variance estimated from sampling:

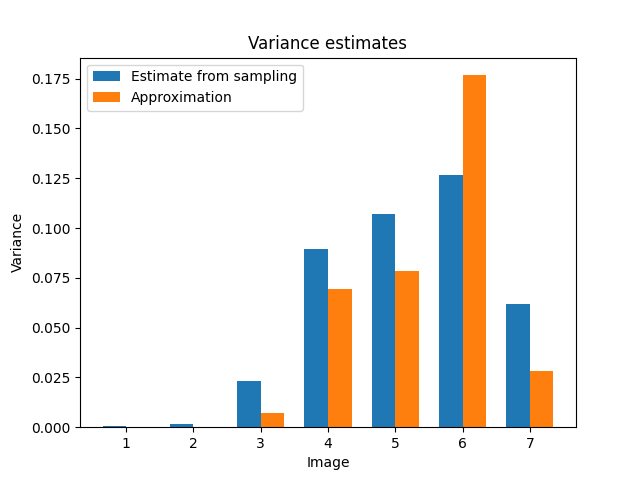
We can see that the approximated variance is not exactly equal to the variance estimated from sampling, but it is generally higher for images that are not similar from the training set.

This can be used as a rough indicator, when the prediction of MobileNet might not be trusted.

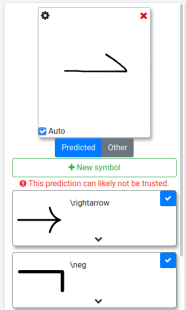
In the Detext app this looks like this:

.

Bibliography

Yarin Gal and Zoubin Ghahramani. Dropout as a bayesian approximation: representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on International Conference on Machine Learning - Volume 48, ICML'16, 1050–1059. JMLR.org, 2016. URL: https://dl.acm.org/doi/10.5555/3045390.3045502. ↩

Andrew G. Howard, Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. Mobilenets: efficient convolutional neural networks for mobile vision applications. CoRR, 2017. URL: http://arxiv.org/abs/1704.04861, arXiv:1704.04861. ↩

Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and scalable predictive uncertainty estimation using deep ensembles. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS'17, 6405–6416. Red Hook, NY, USA, 2017. Curran Associates Inc. URL: https://dl.acm.org/doi/10.5555/3295222.3295387. ↩

Mattia Segù, Antonio Loquercio, and Davide Scaramuzza. A general framework for uncertainty estimation in deep learning. CoRR, 2019. URL: http://arxiv.org/abs/1907.06890, arXiv:1907.06890. ↩